Field lines
What are field lines?
Field lines are imagined lines that represent the course of a magnetic field. The stronger the magnetic field, the denser the field lines are drawn. You can also draw an arrowhead on the field lines, which then points from the north pole to the south pole of the magnet. In a magnetic field, iron filings arrange themselves along the field lines in linear patterns. Thus, field lines of a magnetic field can be made visible in an experiment.Table of Contents
Magnetic field lines illustrate the magnetic field.
However, they also have real physical meaning because the density of the field lines indicates the strength of the magnetic forces,
and the direction of the field lines shows the direction of the magnetic forces.
If iron filings are sprinkled on a sheet of paper with a magnet underneath, the iron particles arrange themselves in linear patterns and appear to directly trace the magnetic field lines.
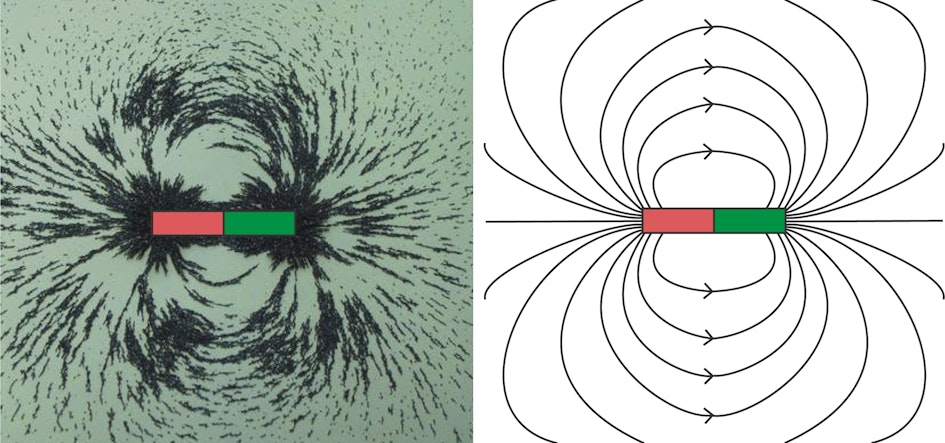
The image on the left shows the result of an experiment where iron filings are sprinkled on a sheet of paper with a rod magnet underneath.
The iron filings appear to arrange themselves along the magnetic field lines.
On the right, the course of the field lines is schematically indicated with the defined direction from the north pole (red) to the south pole (green).
In which direction do magnetic field lines run?
The field lines always run from the north pole to the south pole of a magnet. However, the field lines do not end at the south pole but continue inside the magnet through the material back to the north pole.The reason for this is that there are no sources or sinks of the magnetic field. So, there is no material from which magnetic field lines run out without running back in and vice versa. In physics terms, this means that there are no magnetic charges like positive or negative electrical charges, for example. Only from these sources would magnetic field lines run in a straight line.
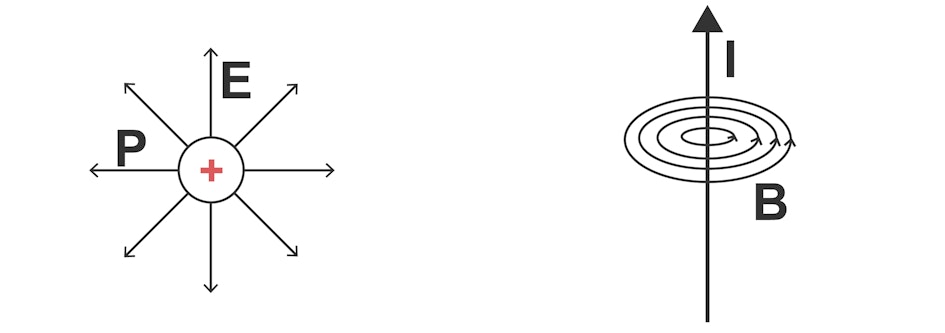
From an electrical charge, the field lines of the electric field E
emanate in a straight line as a so-called 'hedgehog field' (left).
The magnetic flux density B
, on the other hand, always forms closed-loop field lines (right).
The electric and magnetic fields fill the entire space.
The illustration only shows a few field lines schematically to indicate the difference between electric and magnetic fields.
Are magnetic field lines a closed loop?
The B field lines of the magnetic field are closed lines without beginning or end, but they can also extend to infinity. This is because the magnetic field is a vortex field, as described mathematically by Maxwell's equations. As there are no individual magnetic charges, there is no point source from which magnetic field lines could "start their run" as is the case with charges.Magnetic field lines: relevant when considering the force effect of magnets
Field lines are relevant when considering the force effect of magnets. If this force effect is illustrated by the field lines, then the force of a magnet acts on a tiny test magnet tangentially to the field lines. In addition, the strength of the force is proportional to the density of the field lines in the area of the test piece. If you construct the field lines geometrically and look at their density, you can use the field lines to estimate the force of the magnet for certain distances from a test magnet or ferromagnetic material. Conversely, the course of the field lines can be deduced from the force and energy laws of physics.Magnet on a ferromagnetic surface: course of the field lines
If the north pole of a magnet is brought close to a ferromagnetic material (e.g. iron), the field lines penetrate this material. This must be the case because the iron is being magnetised too. The iron directs its south pole, created by magnetisation, towards the north pole of the magnet so that the field lines of the magnet's north pole point directly towards the south pole of the magnetised iron. On the back of the iron body or, more generally speaking, starting from the area of the north pole of the magnetised iron, the field lines then run back to the south pole of the magnet.Why do magnetic field lines run from north to south?
The direction of the magnetic field lines, i.e. the determination that they run from the north pole to the south pole and not the other way round, is a physical convention. Scientifically, it can only be reasoned that there must be two poles. Which of these is the north pole and which is the south pole was simply designated.Why don't field lines cross?
Field lines are a fundamental concept in physics, developed to visualise the invisible forces of electric and magnetic fields or even gravitational fields. They serve as abstract representations that illustrate the direction and strength of these fields at different points in space. The principle that field lines do not cross is based on the logical assumption that only a single, distinct force effect can prevail at a given point in space.In reality, field lines do not physically exist; rather, they are a tool for scientists and engineers to describe and analyse the properties of fields.
The idea that field lines do not cross is based on the mathematical description of fields using vector fields.
In a vector field, each point is assigned a vector that indicates the magnitude and direction of the force at that point.
The uniqueness of these vectors at each point means that it is impossible to have two different directions for the resulting force on ferromagnetic particles (the force effect is represented by field lines) at the same location without violating the fundamentals of vector calculus.
This concept not only helps to visualise and understand the properties of fields, but also enables the application of mathematical and physical laws, such as Gauss's law for electricity and magnetism or Newton's law of gravity.
This enables precise predictions about the behaviour of particles within these fields and forms the basis for the development of technological applications, from electric motors to satellite orbits.
In summary, field lines are an essential tool in physics that makes abstract concepts tangible.
The rule that they do not cross reflects the clarity and consistency of physical laws, even if the field lines themselves are only a model representation.
In electromagnetic fields, field lines therefore represent the direction of the force acting on ferromagnetic materials (in the case of magnetic fields) at every point in space.
They do not cross, as the force has a clear direction at every point in space.
If field lines were to cross, it would imply that at this crossing point, the resulting magnetic force on the particles has two directions simultaneously, i.e.
the particle could randomly move in two different directions, which is not physically inaccurate for macroscopic objects.
When different forces superimpose, a resultant force is produced by the vectorial addition of these two 'partial forces'.
The field line would then point in the direction of this resultant force at this location.
The uniqueness of the force vectors at each point ensures that field lines always run parallel and do not intersect.
This principle helps to understand and visualise the continuous and consistent nature of force fields.
Making magnetic field lines visible
You can make magnetic field lines visible with the help of iron filings. The iron filings arrange themselves in linear patterns in a magnetic field. Rod magnets or horseshoe magnets are often used for such experiments. Below you will find a few suitable products from the supermagnete online shop.You can find inspiration for fascinating experiments in the project Field lines in 3D or in the video linked below.


Author:
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.hu). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to
[email protected]
© 2008-2024 Webcraft GmbH
© 2008-2024 Webcraft GmbH




